CMU_15-445_PROJECT#2

这个实验2真的是折磨死我了。

Tree Index

索引是一个排序的列表，在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址，在数据十分庞大的时候，索引可以大大加快查询的速度，这是因为使用索引后可以不用扫描全表来定位某行的数据，而是先通过索引表找到该行数据对应的物理地址然后访问相应的数据。

hash table的时间复杂度是$O(1)$。在B+ Tree中，因为它是平衡的，所以它的时间复杂度始终是$O(log n)$，也就是说，对于一个叶子结点上的任何key来说，不管它距离根节点有多远，时间复杂度始终是$O(logn)$，不管我们删除多少次，插入多少次，修改周围的东西，它始终是$O(logn)$。对于一个多路查找树（M-way search tree）而言，在树中的每个节点处，它可以通过$>=M$条不同的路线到达其他节点，它是完美平衡的，当我在对树进行修改时，该数据结构会始终保持平衡性，也就是说任何叶子节点到根节点始终是$O(logn)$，我们还要维护的一件事是，保证每个节点至少都是半满的状态（Andy教授课程讲义），MySQL的InnoDB引擎就是默认B+树索引，自适应hash 索引，但是哈希索引失去了有序性：无法用于排序和分组，只支持精确查找、无法用于部分查找和范围查找。

值得注意的是，hash索引一般用于精确查找，B+树索引更适合范围查找。下面就是建立索引的SQL语句：

-- 在normal_table表的id列建立名为normal_index的普通索引
create index normal_index on normal_table(id); 

---

B树

B树是一种多路平衡查找树，其定义如下：

• 每个节点最多有m-1个关键字
• 根节点最少可以只有1个关键字
• 非根节点至少有m/2个关键字
• 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它
• 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同
• 每个节点都存有索引和数据，也就是对应的key和value

所以，根节点的关键字数量范围：$1<=k<=m-1$，非根节点的关键字数量范围：$m/2<=k<=m-1$，其中m为阶数，表示了一个节点最多有多少个孩子节点。比如有一个5阶的B树，根节点数量范围：$1<=k<=4$，非根节点数量范围：$2<=k<=4$。

B树插入操作

插入的时候，我们需要记住一个规则：判断当前节点key的个数是否小于等于m-1，如果满足，直接插入即可，如果不满足，用节点的中间key将这个节点分为左右两部分，中间的节点放到父节点中即可。如下例子（例子来源于博客)：

在5阶B树中，节点最多有4个key，最少有2个key。

• 插入18，70，50，40

  

• 插入22

  

插入22时，发现这个节点的关键字已经大于4了，所以需要进行分裂，分裂的规则在上面已经讲了。分裂之后如下：

• 接着插入23，25，39

  

• 分裂之后如下：

  

B树删除操作

B树的删除操作相对于一个插入操作是相对复杂一些的，如下面例子：

• 现在有一个初始状态是下面这样的B树，然后进行删除操作：

  

• 删除15，这种情况是删除叶子节点的元素，如果删除之后，节点数还是大于m/2，这种情况只要直接删除即可。

  

​

• 接着，我们把22删除，这种情况的规则，22是非叶子节点，对于非叶子节点的删除，我们需要用后继key（元素）覆盖要删除的key，然后在后续key所在的子支中删除该后继key。对于删除22，需要将后继元素24移动到被删除的22所在的节点。对于删除22,需要将后继元素24移到被删除的22所在的节点。

  

  

• 此时我们发现26所在的节点只有一个元素，小于2（m/2)个，这个节点不符合要求，这时候的规则就是向兄弟节点借元素，如下图所示：

  

• 移动之后，跟兄弟节点合并

  

B+树

B+树其实和B树是非常相似的，我们可以看看相同点。

• 根节点至少一个元素
• 非跟节点元素范围：$m/2<=k<=m-1$

不同点

• B+树有两种类型的节点：内部节点和叶子节点，内部节点就是非叶子节点，内部节点不存储数据，只存储索引，数据都存储在叶子节点。
• 内部节点的key都按照从小到大的顺序排列，对于内部节点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子节点中的记录也按照key的大小排列。
• 每个叶子节点都存有相邻叶子节点的指针，叶子节点本身依关键字的大小自小而大顺序链接。
• 父节点存有右孩子第一个元素的索引。

如下图所示：

插入操作

对于插入操作很简单，只需要记住一个技巧即可：当节点元素数量大于m-1的时候，按中间元素分裂成左右两部分，中间元素分裂到父节点当作索引存储，但是，本身中间元素还是分裂右边这一部分。

下面以一颗5阶B+树的插入过程为例，5阶B+树的节点最少2个元素，最多4个元素。

• 插入5，10，15，20

  

• 插入25，此时元素数量大于4个了，分裂

  

• 接着插入26，30，继续分裂

  

​

删除操作

对于删除操作是比B树简单一些的，因为叶子节点有指针的存在，向兄弟节点借元素时，不需要通过父节点了，而是可以通过兄弟节点移动即可（前提是兄弟节点的元素大于m/2），然后更新父节点的索引；如果兄弟节点的元素不大于m/2（兄弟节点也没有多余的元素），则将当前节点和兄弟节点合并，并且删除父节点中的key，下面我们看看具体的实现：

• 初始状态

  

• 删除10，删除后，不满足要求，发现左边兄弟节点有多余的元素，所以去借元素，最后，修改父节点索引。

  

• 删除元素5，发现不满足要求，并且发现左右兄弟节点都没有多余的元素，所以，可以选择和兄弟节点合并，最后修改父节点索引。

  

• 发现父节点索引也不满足条件，所以，需要做跟上面一步一样的操作

  

B+树相对于B树有一些优势，如下：

• 单一节点存储的元素更多，使得查询的IO次数更多，所以也就使得它更适合作为数据库MySQL的底层数据结构。
• 所有的查询都要查找到叶子节点，查询性能是稳定的，而B树每个节点都可以查找到数据，所以不稳定。
• 所有的叶子节点形成了一个有序链表，更便于查找。
• B+树的空间利用率更高，可减少I/O次数，磁盘读写代价更低。
• 增删文件时，效率更高，因为B+树的叶子节点包含所有关键字，并以有序的链表结构存储，这样可以很好的增删效率。

---

在这里插入红黑树的知识点：

要理解红黑树，我觉得还是要和二叉搜索树、AVL树结合起来理解。

我们都知道，二叉搜索树的性质是顺序存储，缺点是不平衡，在极端情况下会变成链表；AVL树的性质是平衡，如果我们将二者的性质结合起来，就成了红黑树的雏形，红黑树按照顺序存储，还可以保持一定的平衡（放弃了AVL树绝对平衡的性质，而是根据自身红黑的性质保持相对平衡，插入与删除时会比AVL树更方便），这样就稳定了查询时间。

红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质：

性质1：每个节点要么是黑色，要么是红色。

性质2：根节点是黑色。

性质3：每个叶子节点（NIL）是黑色。

性质4：每个红色结点的两个子结点一定都是黑色。

性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点。（保证这棵树尽量是平衡的。）

---

TASK #1 - B+TREE PAGES

我们首先要了解B+树中的key-value映射，key是我们要找的关键字，value指向下一个节点。内部节点的key都按照从小到大的顺序排列，对于内部节点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子节点中的记录也按照key的大小排列。父节点存有右孩子第一个元素的索引。

B+TREE PARENT PAGE

这是内部页和叶页都继承的父类，它只包含两个子类共享的信息。即所有的节点都复用一个header数据域类，其定义在b_plus_tree_page.h中，我们先来看看如下定义：

Variable Name	Size	Description
pagetype	4	Page Type (internal or leaf)//页面类型，内部页或者叶子页
lsn_	4	Log sequence number (Used in Project 4)//日志序列号？
size_	4	Number of Key & Value pairs in page//页面键值对的数量
maxsize	4	Max number of Key & Value pairs in page//键值对最大数
parentpage_id	4	Parent Page Id//父页面ID
pageid	4	Self Page Id//页面ID

在这里我们要实现一些简单的set和get函数，因为非常简单，所以就不列举出来了，但是有一个函数不太简单，那就是GetMinSize函数，正如我们在前面所说的，根节点可以拥有少于半数的元素，而且根节点也有可能是叶节点。我们知道，内部节点的array中的第一个键值对中的键是不可用的，正如下图所示：

我们发现键总是比值少一个。所以说，如果是根节点且根节点是内部节点，那么可以拥有最少2个数组项，其中第0项是无效key的那个；如果是根节点且根节点是叶子节点，那么最少有1个数组项。

在这种情况下，要想实现就很难了，所以我一开始直接简单粗暴的用内部节点来编写这个函数，如下所示：

int BPlusTreePage::GetMinSize() const {return max_size_/2;}

不出意外是会在后续的测试中出错，所以我们改一下：

int BPlusTreePage::GetMinSize() const {
  if(IsRootPage()){
    return IsLeafPage()?1:2;
  }
  if(IsLeafPage()){
    return ceil(max_size_);
  }
  return ceil(max_size_-1)/2+1;
}

B+TREE INTERNAL PAGE

我们可以先了解一下内部节点的声明，如下所示：

/**
 * Store n indexed keys and n+1 child pointers (page_id) within internal page.
 * Pointer PAGE_ID(i) points to a subtree in which all keys K satisfy:
 * K(i) <= K < K(i+1).
 * NOTE: since the number of keys does not equal to number of child pointers,
 * the first key always remains invalid. That is to say, any search/lookup
 * should ignore the first key.
 *
 * Internal page format (keys are stored in increasing order):
 *  --------------------------------------------------------------------------
 * | HEADER | KEY(1)+PAGE_ID(1) | KEY(2)+PAGE_ID(2) | ... | KEY(n)+PAGE_ID(n) |
 *  --------------------------------------------------------------------------
 */

在这个声明当中，我们可以得知，内部节点会有n个key和n+1个page_id，所以，为了使得key和value对应，第一个key是无效的，任何的search/lookup必须忽略第一个key。其实啊，这第一个key我们可以理解为header，父节点的指针就是指向这里。

• 获取/设置key的函数，如下所示：

  INDEX_TEMPLATE_ARGUMENTS
  KeyType B_PLUS_TREE_INTERNAL_PAGE_TYPE::KeyAt(int index) const {
    // replace with your own code
    KeyType key=array_[index].first;
    return key;
  }
  
  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_INTERNAL_PAGE_TYPE::SetKeyAt(int index, const KeyType &key) {
    array_[index].first=key;
  }

• 接着是通过value获取index和通过index获取value，如下所示：

  INDEX_TEMPLATE_ARGUMENTS
  int B_PLUS_TREE_INTERNAL_PAGE_TYPE::ValueIndex(const ValueType &value) const {
    int index=0;
    while(array_[index].second!=value){
      index++;
    }
    return index;
  }
  
  INDEX_TEMPLATE_ARGUMENTS
  ValueType B_PLUS_TREE_INTERNAL_PAGE_TYPE::ValueAt(int index) const {
    ValueType value=array_[index].second;
    return value;
  }

• 接着是通过key从当前节点查找下一节点，如下所示（具体实现看代码注释）：

  INDEX_TEMPLATE_ARGUMENTS
  ValueType B_PLUS_TREE_INTERNAL_PAGE_TYPE::Lookup(const KeyType &key, const KeyComparator &comparator) const {
    //采用二分查找
    int left=1;
    int right=GetSize()-1;
    int mid;
    while(left<=right){
      mid=left+(right-left)/2;
      int res=comparator(array_[mid].first,key);
      if(res==0){//如果找到直接返回
        return array_[mid].second;
      }
      if(res<0){
        left=mid+1;
      }
      if(res>0){
        right=mid-1;
      }
    }
    int target=left;
    //如果key比array中的所有key都大，就返回最后一个key的value
    if(target>=GetSize()){
      return array_[GetSize()-1].second;
    }
    //否则返回target-1的value
    return array_[target-1].second;
  }

• 我们先来实现CopyNFrom函数，这个函数的意思就是最简单的插入操作，至于其他更复杂的操作则在其他函数实现。那么这就很简单了，我们可以直接将key-value插入进去。在这里我们用到了copy函数，我们来说一说:

  std::copy(iterator source_first, iterator source_end, iterator target_start);

  在这里，我们设置source_first=items，设置source_end=items+size，设置目标迭代器为array_，这样我们就将items到items+size的元素复制到了array。

  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_INTERNAL_PAGE_TYPE::CopyNFrom(MappingType *items, int size, BufferPoolManager *buffer_pool_manager) {
    std::copy(items,items+size,array_);
    IncreaseSize(size);
  }

• 然后是PopulateNewRoot函数，这里模拟的是新建一个root页面，在上面我们已经将过了，直接贴代码：

  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_INTERNAL_PAGE_TYPE::PopulateNewRoot(const ValueType &old_value, const KeyType &new_key,const ValueType &new_value) {
    //oldvalue为第一个值
    array_[0].second=old_value;
    //后面一对键值对
    SetKeyAt(1,new_key);
    array_[1].second=new_value;
    IncreaseSize(2);
  }

• InsertNodeAfter函数，在old_value后面加入新的key-value对，如下所示：

  INDEX_TEMPLATE_ARGUMENTS
  int B_PLUS_TREE_INTERNAL_PAGE_TYPE::InsertNodeAfter(const ValueType &old_value, const KeyType &new_key,const ValueType &new_value) {
    //在旧的value之后插入新的key-value
    int index= ValueIndex(old_value);
    for(int i=GetSize()-1;i>index;i--){
      array_[i+1]=array_[i];
    }
    array_[index+1]={new_key,new_value};
    IncreaseSize(1);
    return GetSize();
  }

• 然后我们来实现分裂操作，也就是节点中元素数量大于Max_Size时，我们需要做的操作，如下图所示。其中，recipient是分裂出来的page，，分裂的时候移动一半键值对去recipientpage，这个时候当前page的键值对数量是等于M的。

  

  代码如下：

  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_INTERNAL_PAGE_TYPE::MoveHalfTo(BPlusTreeInternalPage *recipient,BufferPoolManager *buffer_pool_manager) {
  	  // 拷贝
    int last_index = GetSize() - 1;
    int start = last_index / 2 + 1;
    int i = 0;
    int j = start;
    while (j <= last_index) {
      recipient->array_[i].first = array_[j].first;
      recipient->array_[i].second = array_[j].second;
      i++;
      j++;
    }
  
    // 维护size
    SetSize(start);
    recipient->SetSize(last_index - start + 1);
  
    // 维护孩子节点的parent_page_id，根据valueat函数得到page_id，子节点的page_id，
    for (int i = 0; i < recipient->GetSize(); i++) {
      auto page_id = recipient->ValueAt(i);
      auto page = buffer_pool_manager->FetchPage(page_id);
      BPlusTreePage *bp = reinterpret_cast<BPlusTreePage *>(page->GetData());
      bp->SetParentPageId(recipient->GetPageId());
      buffer_pool_manager->UnpinPage(page_id, true);
    }
  }

• 对于删除操作，我们首先要实现Remove函数，利用copy函数实现，这里就不贴代码了。

• 接下来我们重点要实现的就是这几个Move函数，对于这几个函数，我们会用到第一个实验中的buffer_pool_manager，我们挑一个函数进行讲解。

  对于MoveAllTo函数，我们要将节点中的所有键值对删除到“收件人”节点。此外我们还要将孩子节点的父节点转化为recipient，

​ 除此之外，我们还要将该节点的父节点的子节点换成recipient。代码如下所示：

INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_INTERNAL_PAGE_TYPE::MoveAllTo(BPlusTreeInternalPage *recipient, const KeyType &middle_key,
                                               BufferPoolManager *buffer_pool_manager) {
  auto parent_page = reinterpret_cast<B_PLUS_TREE_INTERNAL_PAGE_TYPE *>
  (buffer_pool_manager->FetchPage(GetParentPageId())->GetData());

  for(int i = 0; i< GetSize(); i++){
    //获取孩子节点页面
    auto page = buffer_pool_manager->FetchPage(array_[i].second);
    auto child_page = reinterpret_cast<BPlusTreePage *>(page->GetData());
    //将孩子节点页面的父节点转换为recipient
    child_page->SetParentPageId(recipient->GetPageId());
    buffer_pool_manager->UnpinPage(child_page->GetPageId(), true);
  }


  int prior_size = recipient->GetSize();
  recipient->SetKeyAt(prior_size, middle_key);
  recipient->SetValueAt(prior_size, ValueAt(0));
  recipient->IncreaseSize(1); //注意别忘了更新

  recipient->CopyNFrom(array_+1, GetSize()-1, buffer_pool_manager);
  SetSize(0);
  buffer_pool_manager->UnpinPage(parent_page->GetPageId(), true);
}
	

B+TREE LEAF PAGE

在这里leafpage的value是RID，什么是RID呢？RID=page_id + slot number。

• 一些简单的set/get函数，代码如下所示：

  INDEX_TEMPLATE_ARGUMENTS
  page_id_t B_PLUS_TREE_LEAF_PAGE_TYPE::GetNextPageId() const { return next_page_id_; }
  
  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_LEAF_PAGE_TYPE::SetNextPageId(page_id_t next_page_id) {
    next_page_id_=next_page_id;
  }

• KeyIndex函数要求我们找到第一个大于key的元素的索引，我们还是可以用二分法进行查找，代码如下所示，这里就不写注释了：

  INDEX_TEMPLATE_ARGUMENTS
  int B_PLUS_TREE_LEAF_PAGE_TYPE::KeyIndex(const KeyType &key, const KeyComparator &comparator) const {
    int left=0;
    int right=GetSize()-1;
    while(left<=right){
      int mid=left+(right-left)/2;
      int res=comparator(key,array_[mid].first);
      if(res==0){
        return mid;
      }
      if(res>0){
        left=mid+1;
      }else{
        right=mid-1;
      }
    }
    return right+1;
  }

• 返回index对应的key，以及返回index对应的key-value对，如下所示：

  INDEX_TEMPLATE_ARGUMENTS
  KeyType B_PLUS_TREE_LEAF_PAGE_TYPE::KeyAt(int index) const {
    // replace with your own code
    KeyType key = array[index].first;
    return key;
  }
  
  INDEX_TEMPLATE_ARGUMENTS
  const MappingType &B_PLUS_TREE_LEAF_PAGE_TYPE::GetItem(int index) {
    return array[index];
  }

• leafpage的插入操作，我们用上文中的KeyIndex函数找到相应的index，然后插入进去，代码如下所示：

  INDEX_TEMPLATE_ARGUMENTS
  int B_PLUS_TREE_LEAF_PAGE_TYPE::Insert(const KeyType &key, const ValueType &value, const KeyComparator &comparator) {
    int index=KeyIndex(key,comparator);
    for(int i=GetSize()-1;i>=index;i--){
      array_[i+1]=array_[i];
    }
    array_[index].first=key;
    array_[index].second=value;
    IncreaseSize(1);
    return 0;
  }

• MoveFirstToEndOf函数：将此页面中的第一个键值对删除到recipient页面。

  在这个函数中要调用CopyLastFrom函数，我们将第一个键值读取出来用CopyLastFrom函数写入recipient中，然后用copy函数将当前page array向右边移动一格。

  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_LEAF_PAGE_TYPE::MoveFirstToEndOf(BPlusTreeLeafPage *recipient) {
    MappingType item=array_[0];
    recipient->CopyLastFrom(item);
    std::copy(array_+1, array_+GetSize(), array_);//当前page元素均向右移动一格
    IncreaseSize(-1);
  }

  相同的道理，MoveLastToFrontOf如下：

  INDEX_TEMPLATE_ARGUMENTS
  void B_PLUS_TREE_LEAF_PAGE_TYPE::MoveLastToFrontOf(BPlusTreeLeafPage *recipient) {
        /*
        * 更新recipient page的信息
        */
    MappingType item=array_[GetSize()-1];
    recipient->CopyFirstFrom(item);
    IncreaseSize(-1);
  }

debug日志（这里就是我debug的心得了，大家不必看，我只是写着凑字数

注意：在此时我还没有完成构建二叉树的任务，这一部分的测试是根据而他人的代码调试的。

大家看这种情况，说明我的max_size并没有设置好，我们来debug：

这里错误就很明显了我们找到对应的位置，原来insert函数写错了,应该返回size但是我误写成返回0了，当我更改后变成这个这个样子：

那么在这里为什么会有两个5呢，被insert了两次？其实这里是test文件中的测试方式，测试插入相同的元素会不会有变化。那么如果我们不准插入相同的key，能不能解决这个问题呢？（这其实是后面生成树的时候的函数中的错误，但是我们还是在leafpage的insert中进行一个判断，更改代码后如下所示：

这个时候我们发现已经基本正确了，但是最后一个叶子节点的指向有问题，所以我们还要debug。

当我看了网上人家的代码后，我发现错误是MoveHalfTo函数，在这个函数中要求我们更新recipient页面的nextpage，当我按照提示设置nextpaage之后却发现出现了上述情况，这到底是哪里错了我暂且蒙古。删除相关语句后如下所示。

当我自己完成了整个b_plus_tree的函数之后，我再次进行测试，发现出现如下错误：

这个错误也是相当离谱的，说明我们设置的min_size没有成功而且只发生在leaf_page，但是我们之前的测试是正确的，也就是说错误应该是在b_plus_tree的函数里面，如果我们这个错误不解决，那么后面的coalesce函数肯定会出错。但先不管了，我们先完成后面的函数。

TASK #2.A - B+TREE DATA STRUCTURE (INSERTION & POINT SEARCH)

在这个任务中我们要实现b_plus_tree.cpp中的函数，才能完成一个完整的b+树结构。（到这里就开始折磨了

在这里补充一下RID的结构，

我们还是先来分析一下给定的b_plus_tree类中的数据结构，如下所示：

// member variable
std::string index_name_;//
page_id_t root_page_id_;//root_page_id,用来引导整个b+树
BufferPoolManager *buffer_pool_manager_;//
KeyComparator comparator_;
int leaf_max_size_;//b+树的叶子节点的最大容量
int internal_max_size_;//中间节点的最大容量

• 首先是IsEmpty函数，对于该函数，我们只要判断root_page_id是否有效就可以判断b+树是否为空，代码如下所示：

  bool BPLUSTREE_TYPE::IsEmpty() const {
    return root_page_id_==INVALID_PAGE_ID;
  }

• IsEmpty函数往往与StartNewTree函数一起调用，对于StartNewTree函数来说，我们首先将root_page_id对应的页面写到buffer pool，然后然后对其进行初始化，将key-value插入进去，最后unpin。关键代码如下所示：

  Page *new_page = buffer_pool_manager_->NewPage(&root_page_id_)//to buffer pool
  LeafPage *leaf_page = reinterpret_cast<LeafPage *>(new_page);
  leaf_page->Init(root_page_id_,INVALID_PAGE_ID,leaf_max_size_);//初始化
  leaf_page->Insert(key, value, comparator_);//insert
  buffer_pool_manager_->UnpinPage(root_page_id_, true);  // unpin

• InsertIntoLeaf函数，将常量键值对插入叶页，用户需要先找到正确的叶子页面作为插入目标，然后再看通过叶子页面查看插入键是否存在。 如果存在，返回，否则插入条目。 如有必要，请记住处理拆分。因为我们只支持唯一键，如果用户尝试插入重复键返回 false，否则返回 true。注意，我们这里判断是否分裂用的是if (leaf_page->GetSize() == maxSize(leaf_page) + 1)。做到这一步，我们发现其实还必须得搞懂FindLeafPage这个函数，那么这个函数咋搞呢？先看其本身的代码：

  //这个时候我是有点疑惑的，如果说这个函数要的是返回参数键所在的页面，但是如果键没有在页面之中应该返回什么呢？如果说键没有在页面之中，那就说明可以插入，这个时候应该怎么插入呢？其实这里的意思只是说返回离参数键最近的页面，所以我们调用的lookup函数。
  INDEX_TEMPLATE_ARGUMENTS
  Page *BPLUSTREE_TYPE::FindLeafPage(const KeyType &key, bool leftMost) {
    throw Exception(ExceptionType::NOT_IMPLEMENTED, "Implement this for test");
  }

  修改之后：

  INDEX_TEMPLATE_ARGUMENTS
  Page *BPLUSTREE_TYPE::FindLeafPage(const KeyType &key, bool leftMost) {
    Page *page = buffer_pool_manager_->FetchPage(root_page_id_);
    BPlusTreePage *node = reinterpret_cast<BPlusTreePage *>(page->GetData());
    //如果说root节点就是叶子节点，那么我们直接返回这个节点？
    if(node->IsLeafPage()){
      return page;
    }
    //如果说不是的话
    while (!node->IsLeafPage()) {//循环查找
      InternalPage *i_node = reinterpret_cast<InternalPage *>(node);//强转为inner节点
      page_id_t child_node_page_id;
      if(leftMost){//这是最理想的情况
        child_node_page_id = i_node->ValueAt(0);//此时已经获取了最左边的page_id了
  
      }else{
        child_node_page_id = i_node->Lookup(key,comparator_);
        
      }
      auto child_page = buffer_pool_manager_->FetchPage(child_node_page_id);//根据id获取页面
      auto child_node = reinterpret_cast<BPlusTreePage *>(child_page->GetData());
      node=child_node;
      page=child_page;
    }
    return page;
  }

  //如果需要新建树
    if (IsEmpty()) {
      StartNewTree(key, value);
      return true;
    }
    // 1. if insert key is exist
    if (leaf_page->Lookup(key, nullptr, comparator_)) {
      buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false); // unpined page
      return false;
    }
    // 1. if insert key is exist
    if (leaf_page->Lookup(key, nullptr, comparator_)) {
      buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false); // unpined page
      return false;
    }
     // 2. insert entry
    leaf_page->Insert(key, value, comparator_);
    
     if (leaf_page->GetSize() == maxSize(leaf_page) + 1) {
      LeafPage *new_leaf = Split(leaf_page);
      InsertIntoParent(leaf_page, new_leaf->KeyAt(0), new_leaf, transaction);
    }

• 我们的Split函数和InsertIntoParent函数是分开的，我们用下面两幅图来解释这个过程：

  

  

  上面这两幅图解释了split和insertintoparent这两个过程。

  在这里，如果说old_node是根节点，那么整棵树直接升高一层，我们创建一个新节点R作为根节点，其关键字为key，左右孩子分别为old_node和new_node，如上图所示。

  if (old_node->IsRootPage()) {  // old node为根结点
     page_id_t new_page_id = INVALID_PAGE_ID;
     //拿一个新的页面到buffer pool，最为新的根节点写入
     Page *new_page = buffer_pool_manager_->NewPage(&new_page_id);
     root_page_id_ = new_page_id;
  // 注意初始化parent page id和max_size
     InternalPage *new_root_node = reinterpret_cast<InternalPage *>(new_page->GetData());
     new_root_node->Init(new_page_id, INVALID_PAGE_ID, internal_max_size_);  
     // 修改新的根结点的孩子指针，即array[0].second指向old_node，array[1].second指向new_node；对于array[1].first则赋值为key
     new_root_node->PopulateNewRoot(old_node->GetPageId(), key, new_node->GetPageId());
     // 修改old_node和new_node的父指针
     old_node->SetParentPageId(new_page_id);
     new_node->SetParentPageId(new_page_id);
  // dirty置为true
     buffer_pool_manager_->UnpinPage(new_page->GetPageId(), true);  
    
     UpdateRootPageId(0); 
     return; 
   }

  如果说old_node不是根结点，我们找到old_node的父节点进行操作，先直接插入(key,new_node->page_id)到父节点，如果插入后父节点满了，则需要对父结点再进行拆分(Split)，并继续递归。

• Split函数中，用户拆分输入页面并返回新创建的页面。使用模板 N 表示内部页面或叶子页面。用户需要首先向缓冲池管理器请求新页面（注意：抛出如果返回值为 nullptr，则会出现“内存不足”异常），然后从输入页面移动一半键值对到新创建页面。

  • 这里说的抛出很好理解：

  Page *new_page = buffer_pool_manager_->NewPage(&root_page_id_);
    if (new_page == nullptr) {
      throw "out of memory";
    }

  • 对于叶子节点来说，我们除了要movehalfto绑定相应的父节点，还要对叶子节点链表进行更新，如下所示：

    new_leaf_node->SetNextPageId(leaf_node->GetNextPageId());
    leaf_node->SetNextPageId(new_leaf_node->GetPageId());

  • 对于内部节点，我们则只进行movehalfto和绑定相应的父节点：

    new_internal_node->Init(new_page_id, internal_node->GetParentPageId(),internal_max_size_);
       internal_node->MoveHalfTo(new_internal_node,buffer_pool_manager_);

• 对于InsertIntoLeaf函数来说

  那么怎么结合InsertIntoLeaf函数和split函数呢？这两个函数的调用主要是发生在insert函数里面，如果插入之后使得page分裂，那么就肯定要调用split函数和insertintoleaf函数。可以参考上面的insert函数。

• 实现GET，分为3步，第一步找到那个叶子的page，在叶子page里找这个key，找到这个key之后放入result中，用完最后unpin 这个page。

• 对于Insert函数，如果树里面还没有数据，调用StartNewTree函数新建，否则调用InsertIntoLeaf函数插入。

• 对于FindLeafPage函数，他的参数为key和leftmost，我们要找到包含key的节点，如果leftmost为true，那么就不管key，而去找到最左边的叶子节点，否则，找到包含key的叶子节点。

  这里我们就可以分成true和false两种情况，如下所示：

  page_id_t next_page_id = leftMost ? internal_node->ValueAt(0) : internal_node->Lookup(key, comparator_);

TASK #2.B - B+TREE DATA STRUCTURE (DELETION)

• 首先我们要在b_plus_tree_leaf函数中完成RemoveAndDeleteRecord函数，根据提示可以很快完成该函数，如下所示：

INDEX_TEMPLATE_ARGUMENTS
int B_PLUS_TREE_LEAF_PAGE_TYPE::RemoveAndDeleteRecord(const KeyType &key, const KeyComparator &comparator) {
  int index= KeyIndex(key,comparator);

  if(index < GetSize() && (comparator(key, array_[index].first) == 0) ) {
    std::copy(array_ + index + 1, array_ + GetSize(), array_ + index);
    IncreaseSize(-1);
  }
  return GetSize();
}

如果删除导致某些页面低于占用率阈值，您的 B+Tree 索引应该正确执行合并或重新分配。

• Coalesce函数，将所有键值对从一个页面移动到其兄弟页面，并通知缓冲池管理器删除此页。 父页面必须调整为

  • 考虑删除信息。 记得处理 coalesce 或
  • 必要时递归重新分配。
  • 使用模板 N 表示内部页面或叶子页面。
  • @param neighbor_node 输入“节点”的兄弟页面
  • @param 来自方法 coalesceOrRedistribute() 的节点输入
  • @param parent 输入“节点”的父页面
  • @return true 表示要删除父节点，false 表示不删除
  • 发生

• 对于AdjustRoot函数，最重要的是判断其是否应该删除掉根节点，这里有两种情况我们是要删除掉根节点的，也就是根节点是leaf_节点且其size为0,或者其不是leaf_page其size为1，至于为什么这样请看我前面的。

  if (old_root_node->IsLeafPage() && old_root_node->GetSize() == 0) {
      root_page_id_ = INVALID_PAGE_ID;
      UpdateRootPageId(false);
      return true;
    }
    if (!old_root_node->IsLeafPage() && old_root_node->GetSize() == 1) {
      auto internal_page = reinterpret_cast<InternalPage *>(old_root_node);
      auto new_root_id = internal_page->RemoveAndReturnOnlyChild();
      auto new_root_page = buffer_pool_manager_->FetchPage(new_root_id);
      auto new_root_node = reinterpret_cast<BPlusTreePage *>(new_root_page);
      new_root_node->SetParentPageId(new_root_id);
      root_page_id_ = new_root_id;
      buffer_pool_manager_->UnpinPage(new_root_node->GetPageId(), true);
      return true;
    }
    return false;

  

​ 结果如上图所示，我们的输入文件中只有一个元素1，当我们删除掉这个元素之后，我们再生成dot文件，就会出现生成文件为空的提示。

debug日志

当我们进行b_plus_tree_leaf_page_test测试时，出现了如下错误：

#0 0x7f4598902c1d in bustub::BPlusTreeLeafPage<bustub::GenericKey<8ul>, bustub::RID, bustub::GenericComparator<8ul> >::Lookup(bustub::GenericKey<8ul> const&, bustub::RID*, bustub::GenericComparator<8ul> const&) const /home/databrains/CLionProjects/bustub-master/src/storage/page/b_plus_tree_leaf_page.cpp:158

这个错误的出现是由于数组越界，而keyindex函数和array_的不当使用确实会引起数组越界，于是我们对其进行一些修改：

INDEX_TEMPLATE_ARGUMENTS
bool B_PLUS_TREE_LEAF_PAGE_TYPE::Lookup(const KeyType &key, ValueType *value, const KeyComparator &comparator) const {
  int pos = KeyIndex(key, comparator);
  if(pos>=GetSize()||comparator(key, array_[pos].first) == 0){
    return false;
  }
  *value=array_[pos].second;
  return true;
}

发现这样是治标不治本，其原因在于我们在检查是否含有key的时候入的value实参往往是nullptr，所以我们给它增加一个判断：

INDEX_TEMPLATE_ARGUMENTS
bool B_PLUS_TREE_LEAF_PAGE_TYPE::Lookup(const KeyType &key, ValueType *value, const KeyComparator &comparator) const {
  int pos = KeyIndex(key, comparator);
  if(pos>=GetSize()||comparator(key, array_[pos].first) != 0){
    return false;
  }
  if(value== nullptr){
    return true;
  }
  (*value)=array_[pos].second;
  return true;
}

我们进行以下测试，其中测试文件为1,2,3,4,5,6：

#./test/b_plus_tree_print_test
> 3 3
> f input.txt
> d 4
> g tree.dot
> q

得到如下结果：

我们发现有两个错误，第一个错误是叶子节点的min_size，第二个错误是没有完全删除掉page，我们先来解决第二个错误：

在这里minsize依然是1，说明是InsertIntoParent或Split函数的错误，当我们的input文件只有一个数据1时，其输出如下：

这也佐证了我们的说法。

当输入为1，2，3，4，5，6的时候，DEBUG如下：

在InsertIntoParent函数中就已经变成这样了，经过多次排查，问题出在Split函数当中，妈的终于找到错误了，原来是GetMinSize写错了。。。

我们现在看到第一个错误，在这里我认为应该删除没有数据的leaf和其父节点中相应的键值对，但其实不删除也没错。健壮的函数会保证其增删查改的正确性，只不过开销会更大。

TASK #3 - INDEX ITERATOR

我们都知道，在B+树中，叶子节点link起来，可以实现快速range scan。在这个任务中，我们要构建一个通用索引迭代器来有效地检索所有叶子页面。其中，Begin函数返回一个状态为初始化的迭代器对象，End返回一个指向结束的迭代器对象。

我们先来看看iterator中的几个成员：

BufferPoolManager *buffer_pool_manager_;//用来操作当前被写入buffer pool的节点
Page *page_;
int index_;
LeafPage *leaf_;

• 对于Begin函数，我们先直接用FindLeafPage找到最左边的节点，如下所示：

  Page *leaf_page = FindLeafPage(KeyType(), true);
  return INDEXITERATOR_TYPE(buffer_pool_manager_, leaf_page, 0);  

• 对于End函数，入参为void，构造一个代表结束的索引迭代器，叶节点中的键/值对，return : 索引迭代器。我们先找到最左边的叶子节点，然后从最左边移动到最右边。

  Page *leaf_page = FindLeafPage(KeyType(), true);
  LeafPage *leaf_node = reinterpret_cast<LeafPage *>(leaf_page->GetData());
  
  while (leaf_node->GetNextPageId() != INVALID_PAGE_ID) {
      page_id_t next_page_id = leaf_node->GetNextPageId();
      buffer_pool_manager_->UnpinPage(leaf_node->GetPageId(), false);  // page unpinned
  
      Page *next_page = buffer_pool_manager_->FetchPage(next_page_id);  // next_page pinned
      leaf_node = reinterpret_cast<LeafPage *>(next_page->GetData());
    }
  return INDEXITERATOR_TYPE(buffer_pool_manager_, leaf_page, leaf_node->GetSize());

• 重载++，在这个部分的时候，我们可以看看其他模板类中的迭代器++是怎么重载的，在这里我们只要搞清楚leaf range的逻辑就可以了，index代表当前叶子节点中的键值对的序号，如果跳到下一个节点，那么index将从零重新开始运算，最后返回的是当前对象。

  index_++;  
  if (index_ == leaf_->GetSize() && leaf_->GetNextPageId() != INVALID_PAGE_ID) {//如果index等于节点的长度，且节点不是最后一个节点，那么我们就要跳到下一个节点
      Page *next_page = buffer_pool_manager_->FetchPage(leaf_->GetNextPageId());  // pin next leaf page
      buffer_pool_manager_->UnpinPage(page_->GetPageId(), false);  //unpin当前page
      
      page_ = next_page;
      leaf_ = reinterpret_cast<LeafPage *>(page_->GetData());  // 更新到下一个节点
      index_ = 0;                                              // 重置index
    }
    return *this;

• 重载*，这里的返回的是当前的键值对。

  return leaf_->GetItem(index_);//这个没啥好说的，返回相应的key-value就行

• 重载==，怎么判断两个迭代器对象是否相等，我们只需要判断二者的位置是否相等就可以了，也就是先比较二者是否处于同一个叶子节点，再比较二者的index值是否相等。

  INDEX_TEMPLATE_ARGUMENTS
  bool INDEXITERATOR_TYPE::operator==(const IndexIterator &itr) const {
    return leaf_->GetPageId() == itr.leaf_->GetPageId() && index_ == itr.index_;  // leaf page和index均相同
  }

• 重载!=，这里我们直接用之前重载的==就可以了。

  return static_cast<bool>(*this != itr);

TASK #4 - CONCURRENT INDEX

在这部分，您需要更新您原来的单线程 B+Tree 索引，使其能够支持并发操作。我们将使用课堂和教科书中描述的闩锁技术。

在rwlatch.h中，实现了ReaderWriterLatch类，我们看看其成员：

mutex_t mutex_;
cond_t writer_;
cond_t reader_;
uint32_t reader_count_{0};
bool writer_entered_{false};

其中，条件变量writer_和reader_，设置了reader_count，代表读者的引用计数。

我们来看看其底层的函数实现：

void RLock() {
  std::unique_lock<mutex_t> latch(mutex_);
  while (writer_entered_ || reader_count_ == MAX_READERS) {
      //如果上了写锁或者读者达到上限，就等待，这个时候应该是自旋
    reader_.wait(latch);
  }
  reader_count_++;
}

void WLock() {
  std::unique_lock<mutex_t> latch(mutex_);
  while (writer_entered_) {
      //如果上了写锁就不能再上了
    reader_.wait(latch);
  }
  writer_entered_ = true;
  while (reader_count_ > 0) {
      //如果现在还有读者也不能上
    writer_.wait(latch);
  }
}

这个实现挺有意思的。

当我们没有实现并发的时候，在做b_plus_tree_concurrent_test的时候，出错的概率不是一定的，而是根据随机的并发而不确定的，这导致我一会pass 5 test，一会pass 3 test。

所以说当务之急是完成并发。这里我参考了周小伦大神的实现。

INDEX_TEMPLATE_ARGUMENTS
Page *BPLUSTREE_TYPE::FindLeafPageRW(const KeyType &key, bool left_most, enum OpType op, Transaction *transaction) {
  Page *page = buffer_pool_manager_->FetchPage(root_page_id_);  // now root page is pin
  BPlusTreePage *node = reinterpret_cast<BPlusTreePage *>(page->GetData());
  while (!node->IsLeafPage()) {
    if (op == OpType::Read) {
      page->RLatch();
      UnlatchAndUnpin(op,transaction);
    } else {
      // else is write op
      page->WLatch();
      if (IsSafe(node, op)) {
        UnlatchAndUnpin(op, transaction);
      }
    }
    transaction->AddIntoPageSet(page);
    InternalPage *internal_node = reinterpret_cast<InternalPage *>(node);
    page_id_t next_page_id = left_most ? internal_node->ValueAt(0) : internal_node->Lookup(key, comparator_);
    Page *next_page = buffer_pool_manager_->FetchPage(next_page_id);  // next_level_page pinned
    BPlusTreePage *next_node = reinterpret_cast<BPlusTreePage *>(next_page);
    page = next_page;
    node = next_node;
  }
  return page;
}

这是周小伦大神的实现。

如何实现并发

我们来看看Andy在lab中怎么说的（机器翻译）：

• 搜索：从根页面开始，抓住子页面上的读取（R）闩锁，然后在您登陆子页面后立即释放父页面上的闩锁。
• 插入：从根页面开始，抓住子页面的写（W）锁存器。一旦孩子被锁定，检查它是否安全，在这种情况下，不是满的。如果孩子是安全的，则释放祖先的所有锁。
• 删除：从根页面开始，抓住子页面的写（W）锁存器。一旦孩子被锁定，检查它是否安全，在这种情况下，至少半满。 （注意：对于根页面，我们需要用不同的标准检查）如果孩子是安全的，释放所有祖先的锁。

---

我们在B+树的并发控制中要保证以下结果的正确性：

• 逻辑正确性：能否看到应该看到的结果？
• 物理正确性：内部的数据结构表示是否被保护？（比如，在对B+树索引遍历时，当一个线程需要跳转到下一节点时，其它线程有可能会改变B+树的结构，使得指针指向为无效地址）

LATCH CRABBING / COUPLING

这是一个允许多线程同时访问/修改B+树的协议。其基本思想为：

• 获得父节点的latch
• 获得子节点的latch
• 当安全的情况下才释放父节点的latch

在读写锁中，当有一个 线程获得写锁定，其它无论是读锁定还是写锁定都将阻塞直到写解锁；当有一个线程获得读锁定，其它读锁定仍然可以继续；当有一个或任意多个读锁定，写锁定将等待所有读锁定解锁之后才能够进行写锁定。

1. 同时只能有一个线程能够获得写锁定。
2. 同时可以有任意多个线程获得读锁定。
3. 同时只能存在写锁定或读锁定（读和写互斥）。
4. 加入MaxReader，来防止写进程饥饿，也就是读进程太多以至于等待时间过长而对写进程造成明显影响。

---

我们来看读写锁在B+树中的具体表现：

查找38，给根节点上读锁：

当我们来到下一个B节点，给B上了读锁，确保已经安全，释放A的读锁。

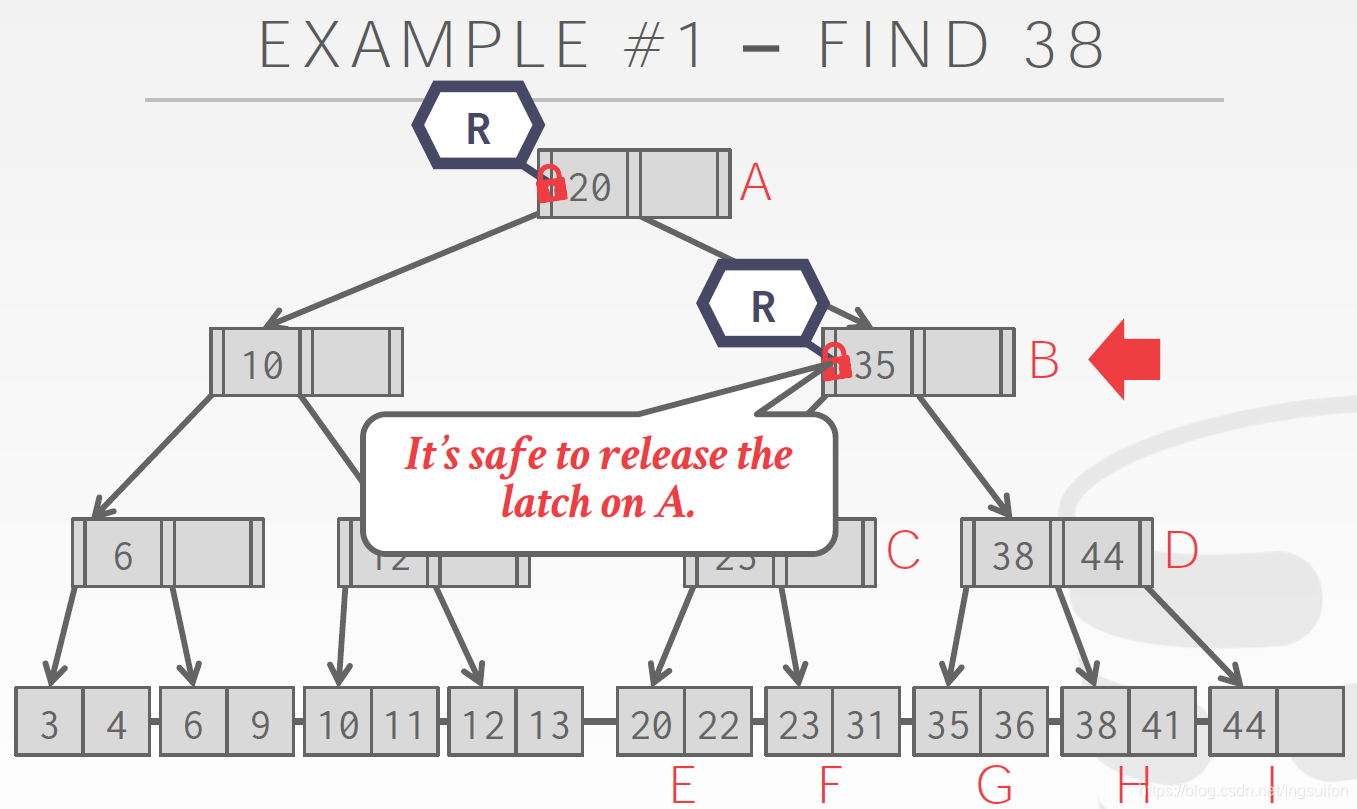
以此类推，找到38。

当我们要删除时，因为我们有可能修改了叶子节点之后会修改内部节点甚至是根节点，因此我们给每一个访问的节点都上写锁。

子节点并没超过半满，所以是不安全的，不能释放父节点的锁。

我们发现此时节点已经超过半满，可以释放祖先节点。

以此类推，直到删除数据并释放所有写锁。

插入操作同理，我们如果发现节点没有半满，就可以释放祖先节点的写锁。

值得注意的是，释放锁时，我们应当从上往下释放，这样可以让等待的线程尽早执行。

我们来开始上锁：

这样做可以实现并发，但是实现不了高并发，要实现高并发还是得优化算法：

---

在上面介绍的操作过程中我们发现：

我们只有在知道了子孙节点是满足特定条件的情况下才能释放祖先节点的写锁，这样可能会造成不必要的阻塞。

我们可以一开始就使用读锁，如果找到一个满足状态的节点就说明该节点的所有祖先节点都不用使用写锁，否则就要使用写锁。

可以使用一个队列，将每次访问的节点入队，给每个节点设置一个标志位，即它的儿子节点是否满足条件。访问完叶子节点之后，我们根据标志位将节点出队。

我们看到上面那副图，我们依次访问ABDH节点，A的儿子节点B不满足条件，将A的标志位设置为0，B的儿子节点满足条件，将B的标志位设置为0，D的儿子节点满足条件，将D的标志位设置为1，叶子节点H的标志位始终为0。这样我们就得到了序列0110（从叶子节点到根节点），我们再搜索一次，找到离叶子节点最近的那个1，设置一个计数器safe_count，这个1和之前的节点都是安全的，然后我们根据计数器再次从根节点访问，就像上面那副图，其实ABD都不用上写锁，我们直接就把队列中110对应的节点DBA都上读锁且访问下一个节点之前马上释放，这样我们就只给最后一个叶子节点上了写锁。

---

改进：

我们可以设置一个缓冲队列，将节点的指针放进去，比如A通过A->array[1].second访问B节点，我们就把这个指针放进去，然后，一旦遇到节点安全，我怕们就把访问这个节点的指针之前入队的指针出队，只留下这个访问这个节点的指针，我们搜索完一遍之后直接通过这个指针搜索这个节点，从这个节点开始上写锁，这样也达到了相同的目的，且开销更小。

INDEX_TEMPLATE_ARGUMENTS
Page *BPLUSTREE_TYPE::FindLeafPageRW(const KeyType &key, bool left_most, enum OpType op, Transaction *transaction,Page *safe_page) {
  Page *page = buffer_pool_manager_->FetchPage(root_page_id_);
    //获取root_page
  BPlusTreePage *node = reinterpret_cast<BPlusTreePage *>(page->GetData());
   
  while (!node->IsLeafPage()) {
      
    if (op == OpType::Read) {//读操作不变
      page->RLatch();
      UnlatchAndUnpin(op,transaction);
    } else {
      // 读锁
      page->RLatch();
      if (IsSafe(node, op)) {
        safe_page=page;//设置safe_page为当前page
      }
    }
    transaction->AddIntoPageSet(page);
    InternalPage *internal_node = reinterpret_cast<InternalPage *>(node);
    page_id_t next_page_id = left_most ? internal_node->ValueAt(0) : internal_node->Lookup(key, comparator_);
    Page *next_page = buffer_pool_manager_->FetchPage(next_page_id);  // next_level_page pinned
    BPlusTreePage *next_node = reinterpret_cast<BPlusTreePage *>(next_page);
    page = next_page;
    node = next_node;
  }
  
  return page;
}

---

这样看似操作更多，但是我们上的是读锁，只是为了防止被其他进程写入，比第一种方案一直上写锁要更好我觉得，特别是在数据量很大和读进程更多的时候。

如果我们存储的数据量足够大，我觉得我这个相较于Andy讲的基础算法算是实现了高并发的。